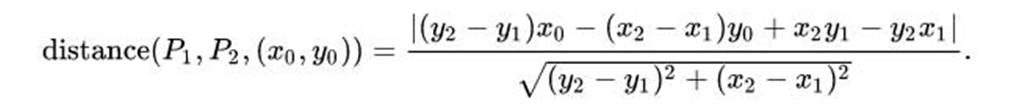GPSで取得した軌跡データには無駄な点も多いので、何とか元の軌跡の形を大きく崩さない方法で間引きたいと、もう何年もまえから考えてきました。
いろいろな人が開発している方法を見てきましたが、簡単なものはどれも一長一短があります。
例えばポイントを50%削減するには、奇数番目のポイントを残し偶数番目のポイントを削除するような、2ポイント毎に1ポイント削除する方法でやっているサイトもあります。この方法は簡単ですが、大事なポイントを削除して軌跡の形が大きく崩れる原因にもなりそうな気がします。
色々見てきた中で、最も合理的だと思ったのは「Douglas-Peucker アルゴリズム」というものでした。
Wikipedia には、間引いて行くアニメーションと共に、コードも紹介してありました。それは非常に短い処理でクイックソートと同じ要領で再帰的に近似曲線を求めています。
https://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm
英語版ですからChromeの翻訳機能の日本語と英語を行ったり来たりしながら、真ん中辺りの「Algorithm」の項目のアニメーションと、その下にある「Pseudocode」項目のコードで、やっていることは理解できました。
原理はアニメーションを分解すると
- 先頭と最後の点をプロット対象にする。
- この2点で線をひく。
- 線から近似精度(ε)以上離れた点を探し、その中で最も遠い点をプロット対象にする。
- プロット対象の各点を線でつなげる。
- 再帰的に ステップ3とステップ4を繰り返す。
ということになり、この流れを図にまとめると下記のようになります。
| 元の形 | 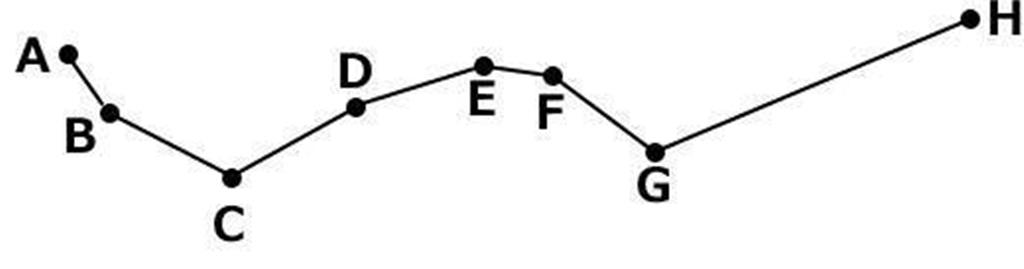 | 最初に近似精度(ε)を決めます。 先頭と最後の点をプロット対象に して2点に線を引く。(AH) |
| ステップ1 | 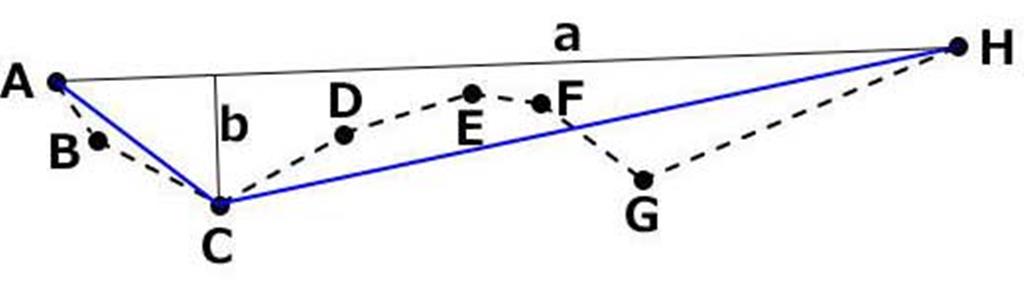 | 線から近似精度(ε)以上離れた点を 探しその中で最も遠い点(C)を プロット対象にする。 |
| ステップ2 | 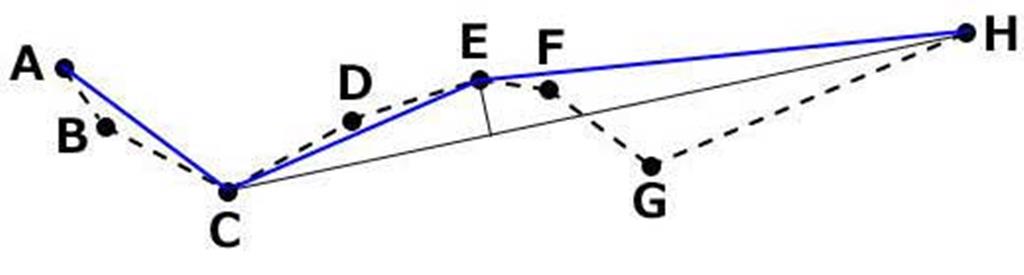 | プロット対象の各点を線でつなげる。 (AC,CH) 近似精度(ε)以下の点(B)は削除対象。 |
| ステップ3 | 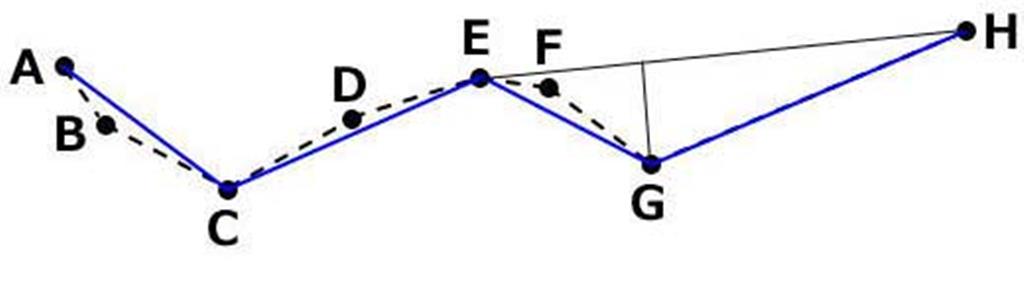 | 同様に線から近似精度(ε)以上離れた 点(G)をプロット対象にする。 |
| ステップ4 | 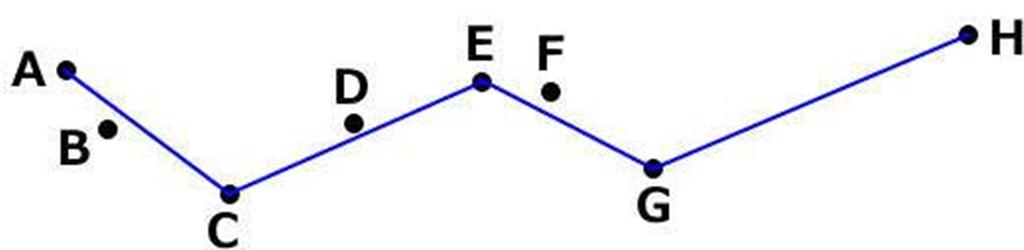 | 得られた結果。 線から近似精度(ε)以上離れていない 3点(B,D,F)が省かれた。 |
ここで、最初に設定する近似精度(ε)は、線からどれだけ離れている点を削除するか、残すかを決める値で、これを大きくすれば間引かれる点が多くなる一方、GPS軌跡の線の形は、元の形から崩れる度合いが大きくなります。最適値は試行錯誤するしかないように思います。
Wikipedia に書いてあったコードは下記です。
■ wikipedia のコード
function DouglasPeucker(PointList[], epsilon)
//Find the point with the maximum distance
dmax = 0
index = 0
for i = 2 to (length(PointList) - 1)
d = PerpendicularDistance(PointList[i], Line(PointList[1], PointList[end]))
if d > dmax
index = i
dmax = d
end
end
//If max distance is greater than epsilon, recursively simplify
if dmax >= epsilon
//Recursive call
recResults1[] = DouglasPeucker(PointList[1...index], epsilon)
recResults2[] = DouglasPeucker(PointList[index...end], epsilon)
// Build the result list
ResultList[] = {recResults1[1...end-1] recResults2[1...end]}
else
ResultList[] = {PointList[1], PointList[end]}
end
//Return the result
return ResultList[]
endまたまたネットを検索しました。
三角形の3辺の長さが分かれば面積を計算できるヘロンの公式が簡単そうです。面積が分かれば三角形の高さは簡単に計算できます。
https://www.wikihow.jp/三角形の高さを求める
https://ja.wikipedia.org/wiki/点と直線の距離
ここで、上記の2番目のWikipediaの「デカルト座標における距離」の2番目の記事の「直線が通る2点によって定義された直線」が、ぴったりそのまま何も考えずに使えそうです。
点 P1=(x1,y1) P2=(x2,y2)の2点を通過する直線と点(x0、y0)の距離は以下で与えられる:上の式を使った具体例がこれです。分母は、点P1と点P2の距離である。分子は、直線上の2点と点(x0,y0)を頂点とする三角形の面積の2倍になっている(参照:en:Area of a triangle#Using coordinates)。
この公式は、三角形の面積を求める公式 A = 1/2bhを変形して得られる h = 2A/b と同値である。但しbは三角形の底辺の長さを、hはその底辺に対する三角形の高さを表す。
引用元:https://ja.wikipedia.org/wiki/点と直線の距離
https://github.com/nkrode/RedisLive/blob/master/src/api/util/RDP.py
これは、コメントアウトの方法を見ると、たぶん「Python」で書いていると思います。「Python」は使ったことがないし、今から勉強する気にもならないので、これを参考にPHPかVBScriptで書き直してみたいと思います。
また、「Douglas-Peucker アルゴリズム」の原型は、どれも近似精度(ε)を指定する方法です。
これは、間引いた結果が何ポイントになるのか事前には分かりません。その部分を改良したアルゴリズムを考えいる人がいました。
以前から時々覗いてみている「TrailNote」というサイトです。
このサイトのオナーは相当な人らしく、私がやりたいと思っていることを既に全てやっている達人です。教えを請いたいところですが、この人はWindowsではなくMacでした。
その人の考えたアルゴリズムは
- ルートの始点と終点をプロット対象とし、確定リストに追加する。
- 始点と終点をつなげた直線から、最も離れた点を探し、その点を、距離やプロット開始点、終了点の情報と共に、プロット候補リストに追加する。
- プロット候補リストから、最も距離の遠い点について取り出し、その点を確定リストに入れる。
- その点より前の部分、後ろの部分を調べ、それぞれ最も離れた点を探し出し、その点を、距離やプロット開始点、終了点の情報と共に、プロット候補リストに追加する。
- 3から4を繰り返す。
- 確定リストの点の数が目標数に到達したら、終了。
具体的な方法は、AからHまでの点を例にすると
| ステップ | ポイント図 | プロット候補リスト | 確定リスト |
|---|---|---|---|
| ステップ1 | 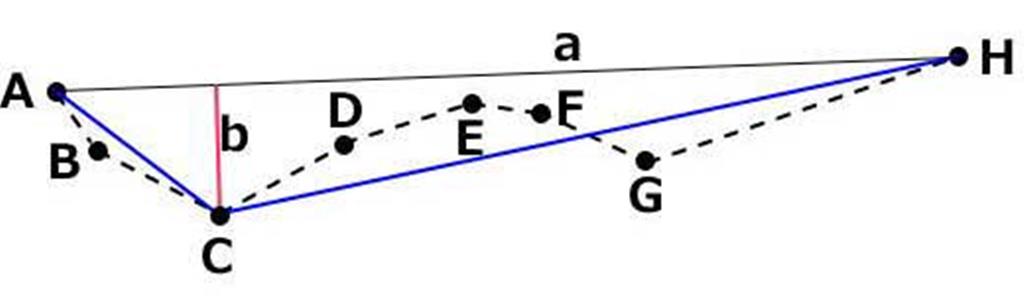 | C | A,H |
| ステップ2 | 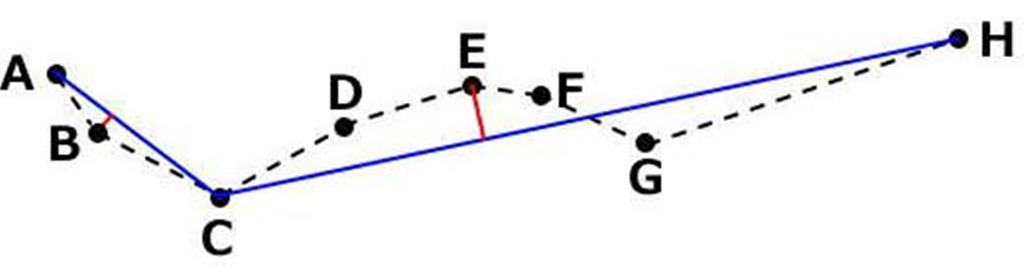 | E,B | A,C,H |
| ステップ3 | 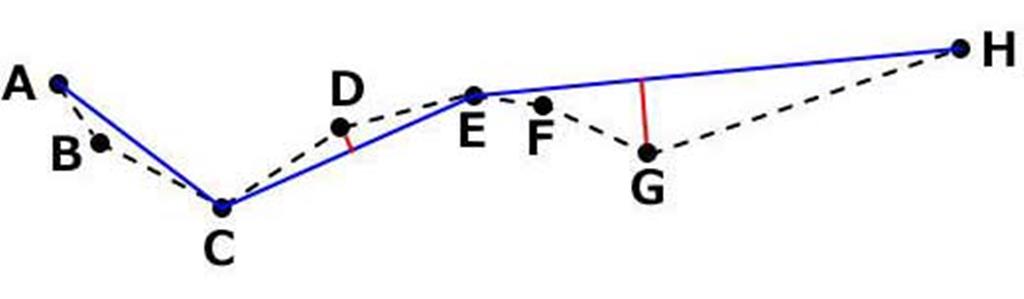 | G,B,D | A,C,E,H |
| ステップ4 | 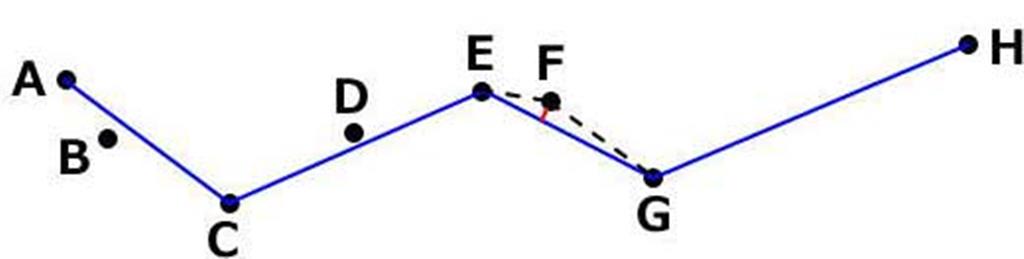 | B,F,D | A,C.E.G,H |
このようにして、最も距離が遠い点から確定させていき、指定した数の点数になるまで続けることで、点数の指定ができるようにしているそうです。素晴らしい!!
プロット候補リストの中は、距離の遠い順で、点が並びます。
この方法では、どんなに近い点でも候補リストに入ります。そのため、Douglas-Peuckerアルゴリズムでは、真っ先に廃棄された点Bも候補リストに入っています。しかし、点Bは距離が近いため、後から追加された点EやGよりも後回しにされます。
もし、1000ポイントのデータを間引いて半分にした場合、確定リストには500ポイント。プロット候補リストには500ポイントが並ぶことになります。
上図の場合、5点を残す場合はステップ4まで、4点を残す場合はステップ3まで、6点を残す場合は、候補リストの中で一番順位が高い「B点」が確定リストに入ります。
引用元:http://www.trail-note.net/tech/thinout/
これで10年以前から何とかしたいと考えていた「Douglas-Peucker アルゴリズム」の具体化に目途が付いたような気がします。生きている内に何とかなりそうです。